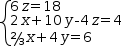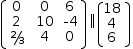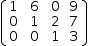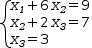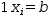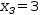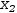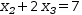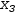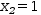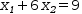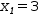5.3 Gaussian Elimination
Systems of linear equations can be solved by placing the
coefficients in a matrix, reducing the matrix to row-echelon form,
and
performing back substitution from the bottom up.
The basis of this
is a theorem attributed to Gauss.
Theorem 5.2
The following operations can be applied to a
linear system without
changing the solution set.
- multiply both sides of an equation by a non-zero constant
- exchange one equation with another
- sum or subtract an equation with (possibly the multiple) of
another
It is possible to apply these rules to the matrix of
coefficients to
produce a new matrix in which the leading non-zero element in
each row is
1, and in which the element below a leading 1 is zero. Such a
matrix is said
to be in row-echelon form. Then new equations can be
recovered from
the new matrix. Finally, back substitution is
performed
to yield a
solution.
Let's try this with the system
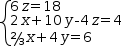 (6⋅z=18, 2⋅x+10⋅y-4⋅z=4, 2/3⋅x+4⋅y=6)ℓ.
(6⋅z=18, 2⋅x+10⋅y-4⋅z=4, 2/3⋅x+4⋅y=6)ℓ.
(1)
Converted to matrix form
[1],
this is
 [(0, 0, 6, 18), (2, 10, -4, 4), (2/3, 4, 0, 6)].
[(0, 0, 6, 18), (2, 10, -4, 4), (2/3, 4, 0, 6)].
Myron always sorts the columns in ascending order of variable name
so
in this matrix the columns represent coefficients
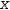 x
x,
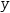 y
y
and
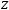 z
z
with the constant in the last column.
Another way of looking at this matrix is as an expression that
concatenates two matrices.
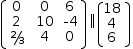 [(0, 0, 6), (2, 10, -4), (2/3, 4, 0)]‖[(, 18), (, 4), (, 6)].
[(0, 0, 6), (2, 10, -4), (2/3, 4, 0)]‖[(, 18), (, 4), (, 6)].
The matrix corresponding to variable coefficients is the left operand
and the column matrix on the right
corresponds to the constants.
Matrices are often combined like this in order to
perform
coordinated
elementary row operations on the individual matrices. A combined
matrix is sometimes
call an
augmented
matrix. The left-hand portion is sometimes called the
unaugmented
matrix.
Suitable application of Gauss' rules in a process called
Gaussian elimination
can reduce the matrix to row-echelon
form, which is
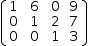 [(1, 6, 0, 9), (0, 1, 2, 7), (0, 0, 1, 3)].
[(1, 6, 0, 9), (0, 1, 2, 7), (0, 0, 1, 3)].
(2)
Note the 1's along the diagonal and the zeroes below the diagonal.
This matrix agrees with
Definition
5.4.
Definition 5.3 A pivot element is the leading non-zero
element in a row of a matrix.
Definition 5.4
A matrix is in row-echelon form if
- rows with at least one non-zero element are above rows
consisting of all zero elements
- For each row, the pivot element is always to the right of the
pivot element in the row above
Matrix
(2)
is a representation of the system of linear equations
[2]
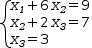 (x_1+6⋅x_2=9, x_2+2⋅x_3=7, x_3=3)ℓ,
(x_1+6⋅x_2=9, x_2+2⋅x_3=7, x_3=3)ℓ,
which is not quite in form of a solution.
To get from the row-echelon form to a final solution, the equations
are worked from last to first.
The last equation is usually in the
form
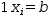 1⋅x_i=b.
For this matrix, the last equation is
1⋅x_i=b.
For this matrix, the last equation is
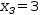 x_3=3.
Working from the second-last to the first, isolate the left side and
substitute
in the right side. That is, isolate
x_3=3.
Working from the second-last to the first, isolate the left side and
substitute
in the right side. That is, isolate
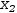 x_2
in
x_2
in
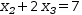 x_2+2⋅x_3=7
[3],
substitute
x_2+2⋅x_3=7
[3],
substitute
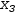 x_3
[4]
and simplify to
x_3
[4]
and simplify to
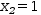 x_2=1.
Then isolate, substitute and simplify
x_2=1.
Then isolate, substitute and simplify
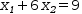 x_1+6⋅x_2=9
to get
x_1+6⋅x_2=9
to get
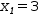 x_1=3.
x_1=3.